Calculating the value of the equilibrium constant (K_c)

This page will hopefully guide and show some common methods you can use to calculate the equilibrium constant K_c for reactions at equilibrium through step-by-step worked examples using a variety of chemical reactions that you are likely to have seen before. So let's go...

Now for any reversible reaction at equilibrium such as the one shown below:

aA_(g) + bB_(g) ⇌ cC_(g) + dD_(g)

Where A and B are the reactants and C and D are the products, while a, b, c and d are the coefficients in the balanced equation for the reaction, we can write an expression for the equilibrium constant for this reaction as:

K_c is the equilibrium constant and the subscript c refers to concentration in mol dm^-3. The square brackets [ ] indicate we are using concentrations in mol dm^-3 for each species included in the expression. How to write expressions for the equilibrium constant K_c and the factors affecting it were covered in detail on the page on equilibrium constants.

Example 1- The Haber process - making ammonia

Calculating equilibrium constants

As an example of how to calculate an equilibrium constant (K_c) let's consider the Haber process for making ammonia. The best place to start when working out the value of an equilibrium constant is by writing a balanced symbolic equation for the reaction and then using it to write an expression for K_c.

A balanced symbolic equation for the Haber process is shown below:

N_2(g) + 3H_2(g) ⇌ 2NH_3(g)

From this balanced symbolic equation we can write the expression for the equilibrium constant, K_c:

Calculating K_c

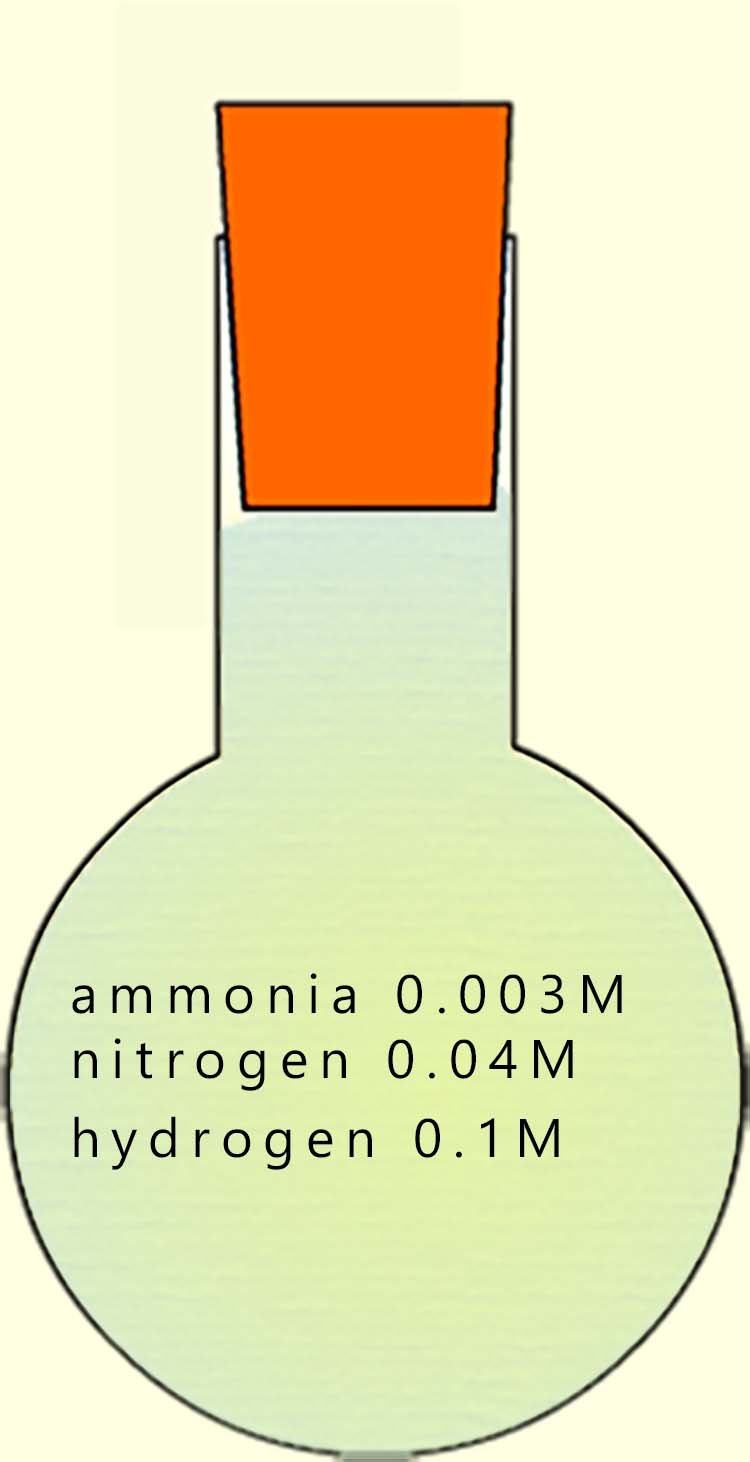
Now suppose we have a sealed flask filled with an equilibrium mixture of nitrogen, hydrogen and ammonia. The equilibrium mixture contains the three gases with the following concentrations:

• [NH₃] = 0.003 mol dm^-3
• [N₂] = 0.04 mol dm^-3
• [H₂] = 0.1 mol dm^-3

To calculate the equilibrium constant for this reaction under the given conditions, substitute these values into the expression for K_c:

The equilibrium constant K_c value of 0.225 is a small number; indicating that the equilibrium mixture contains little ammonia and the position of equilibrium lies very much to the left-hand side.

Example 2 - Preparation of phosphorus pentachloride (PCl₅)

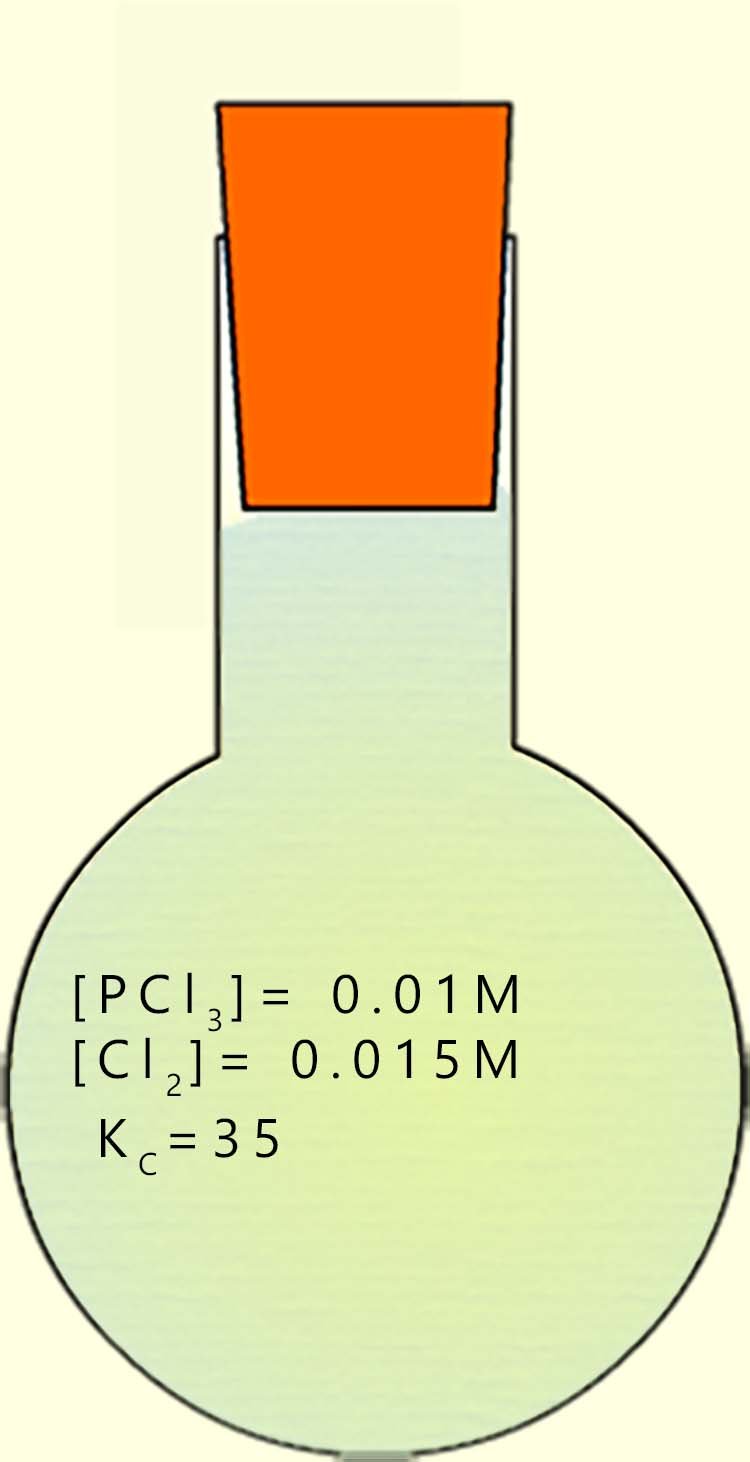
Phosphorus pentachloride (PCl₅) can be prepared by reacting phosphorus trichloride (PCl₃) with chlorine gas (Cl₂) according to the equation below:

PCl_3(g) + Cl_2(g) ⇌ PCl_5(g)

The equilibrium constant K_c for this reaction at the given temperature is 35. The equilibrium concentrations :

• [PCl₃] = 0.01 mol dm^-3
• [Cl₂] = 0.015 mol dm^-3

Calculate the concentration of phosphorus pentachloride; [PCl₅], under the specified conditions. The equilibrium expression for K_c for this reversible reaction is given below. To calculate the concentration of the phosphorus pentachloride we will have to rearrange it to make [PCl₅] the subject of the formula; this is outlined below:

Example 3 - Preparation of the ester ethyl ethanoate

You may remember from your GCSE lessons that esters can be made by reacting a carboxylic acid with an alcohol. The ester ethyl ethanoate can be made by reacting ethanol with ethanoic acid. An equation for this esterification reaction is given below:

ethanoic acid + ethanol ⇌ ethyl ethanoate + water

CH₃COOH + CH₃CH₂OH ⇌ CH₃COOCH₂CH₃ + H₂O

In this worked example we will calculate K_c using an ICE table. Although this is a reaction which involves some liquids we can still use the equilibrium approach by treating all substances as part of one liquid mixture and using concentrations calculated from moles and the total volume of the mixture.

The problem!

Calculate K_c when 0.25 mol of ethanol and 0.25 mol of ethanoic acid are mixed together with a few drops of concentrated sulfuric acid (a catalyst for this reaction) in a sealed flask. The reaction is heated to a constant temperature and allowed to reach equilibrium. The total volume of the system is 50 ml (0.05 dm³) and at equilibrium it was found by titration that there was 0.0825 mol of ethanoic acid present.

The best way to tackle this type of problem is by drawing up a table similar to the one below; it is often called an ICE table (Initial, Change, Equilibrium). You can use it to work out the concentrations of reactants and products before the reaction starts and once it has reached equilibrium.

Initially we have the following numbers of moles of the reactants and products present:

CH₃COOH + CH₃CH₂OH ⇌ CH₃COOCH₂CH₃ + H₂O

   0.25 mol   +    0.25 mol      0 mol     +    0 mol

At equilibrium we know there is 0.0825 mol of ethanoic acid present. Initially there was 0.25 mol, so:

• 0.25 mol - 0.0825 mol = 0.1675 mol of ethanoic acid reacted.

Since 1 mole of ethanoic acid reacts with 1 mole of ethanol, 0.1675 mol of ethanol must also have reacted. From the stoichiometry, this produces 0.1675 mol of the ester and 0.1675 mol of water.

So at equilibrium we have:

CH₃COOH + CH₃CH₂OH ⇌ CH₃COOCH₂CH₃ + H₂O

 0.0825 mol  +  0.0825 mol     0.1675 mol  +  0.1675 mol

We need to convert the number of moles present at equilibrium into concentrations to calculate K_c. To convert moles into concentrations all that we require to know is the total volume of the solution which is 0.05 dm³. Simply use the formula below to calculate the concentrations of all the reactants and products present at equilibrium:

This gives equilibrium concentrations of:

CH₃COOH + CH₃CH₂OH ⇌ CH₃COOCH₂CH₃ + H₂O

0.0825/0.05   +   0.0825/0.05     0.1675/0.05   +   0.1675/0.05

We can now fill in our ICE table using the calculated concentrations, the change in concentration row is filled in last:

To calculate K_c simply substitute the equilibrium concentrations into the expression for K_c:

Example 4 - Calculating equilibrium amounts

As a variation on the ester calculation example above, suppose you mixed together 1 mol of ethanoic acid and 1 mol of ethanol and wanted to know how much ester you would have at equilibrium. We already know K_c for the reaction and the stoichiometry of the equation. We will also assume the temperature stays the same as that in example 3.

Start by writing out a balanced equation to show the number of moles present initially:

CH₃COOH + CH₃CH₂OH ⇌ CH₃COOCH₂CH₃ + H₂O

   1 mol   +     1 mol     ⇌  0 mol     +    0 mol

We do not know how many moles of ester will be produced at equilibrium; we have to calculate this so let’s just say that x moles of ester will be formed at equilibrium. If x mol of ester is formed then we can also say that x moles of water will also be produced and that x moles of ethanoic acid and x moles of ethanol will have been consumed. Therefore at equilibrium we have 1 - x moles of ethanoic acid and 1 - x moles of ethanol:

CH₃COOH + CH₃CH₂OH ⇌ CH₃COOCH₂CH₃ + H₂O

   (1 - x) mol   +    (1 - x) mol   ⇌     x mol     +     x mol

However K_c requires concentrations and not moles so if the volume of the equilibrium mixture is V dm³, then we can say that:

We were able to simplify the equation above by cancelling out all the V for volumes. From worked example 3 above we also know that the equilibrium constant K_c for this reaction is 4.1 (let's just simplify it to 4 to make life easy for ourselves!), so we can say that:

So at equilibrium we have 0.67 mol of ester and water and 0.33 mol (1 - 0.67 moles) of ethanoic acid and ethanol in the equilibrium mixture.

Example 5 - Preparation of hydrogen iodide

You could be asked to calculate an equilibrium constant (K_c) when not all the equilibrium concentrations for the reactants and products are known. However as long as we know the concentrations of the reactants and/or the equilibrium concentration of at least one reactant or product, it is possible to calculate K_c.

As an example, consider the reaction of hydrogen and iodine to form hydrogen iodide:

H_2(g) + I_2(g) ⇌ 2HI_(g)

The problem: A mixture of 5 x 10^-3 mol of hydrogen gas and 1.8 x 10^-3 mol of iodine were placed in a flask with a volume of 5 dm³. The flask was heated to a known temperature and allowed to reach equilibrium. At equilibrium, [HI] was found to be 2.88 x 10^-4 mol dm^-3. Calculate the equilibrium constant (K_c) for this reaction. The standard ICE table for this reaction is set out below:

First convert the number of moles given in the problem into concentrations using the formula below, we know the volume of the flask is 5 dm³:

Then fill in the table with known values:

From the equation, producing 2.88 x 10^-4 mol dm^-3 of HI consumes half that amount of each reactant: (2.88 x 10^-4)/2 = 1.44 x 10^-4 mol dm^-3. So simply fill these values into the ICE table:

Substituting the equilibrium concentrations into the expression for K_c gives: