
The Bohr atom and the quantum mechanical model of the atom
The Bohr atom
The model of the atom we are used to dealing with in GCSE chemistry is called the Bohr atom; named after Neils Bohr
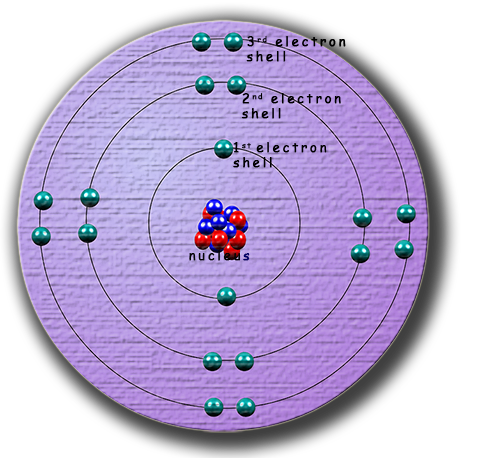
a Nobel Prize winning scientist. This model of the atom assumes a small nucleus with the electrons orbiting the nucleus in circular orbits. Bohr placed the electrons in energy levels or shells, this picture of the atom should be familar to you from your gcse science course. The diagram opposite is probably very familiar to you,
it shows a nucleus which contains the protons and neutrons with the electrons in their shells orbiting the nhucleus in circular orbits. The
first shell holding 2 electrons and the remainder of the shells holding 8 electrons.
The model of the Bohr atom which you will be familar with from gcse science does not offer a completely accurate description
of how the electrons are arranged
in atoms. A new model was put forward by brilliant physcist Edwin Schrodinger in 1926 based on what we now call the quantum
mechanical model of the atom. This new model for the electronic structure of the atom rejects the electron as a particle but instead focuses on
its wavelike properties.
All types of waves can have their properties described using a series of equations,
the solutions to these waves equations are called often called waves functions or orbitals, they are usually
represented by the Greek symbol psi (Ψ). These wave functions provide information about the
position, energy and orientation of the electrons inside atoms. The square of the wavefunction (Ψ2)
is a probability density function which as its name suggests provides the probability of where the
electrons can be found inside the atoms. However the scope of these wave equations is a bit beyond the scope of A-level chemistry and
I have only really mentioned them to wet your appetite! feel free to do a bit of reaseach of your own if you feel the need to, though
I would say do not be put of by the maths required to solve these equations, it is nowhere near as complicated as it looks!
It is important to realise that an orbital is not the
same as an orbit. In the model of the atom from GCSE the electron is imagined as a particle
orbiting the nucleus. However an orbital is a 3d- area in which there is a 95% chance of the
electron being there (remember that the electron is NOT a particle but it behaves as a wave here!).
An orbital is a volume of space around the nucleus where there is an excellent chance or probability
of the electron being found. It is not an orbit!
Quantum numbers
The wave equations from the Schrodinger equation produce 3 quantum numbers that offer a description of the location,
energy and orientation in space of the electrons inside the atom. These quantum numbers are called:
- The principal quantum number (n)- It is perhaps
easy to think of the principal quantum number as the shell or energy level for Bohr atom model we used in gcse chemistry.
Exactly as in gcse science the principal quantum number (n) can have integral values of 1,2,3,4,5.....etc. As n increases
the orbitals are getting larger and the electron is found further from the nucleus.
This means that they are increasing in energy as they increase in size, since separating the electron
(a negative charge) from the nucleus (positive charge) will require energy.
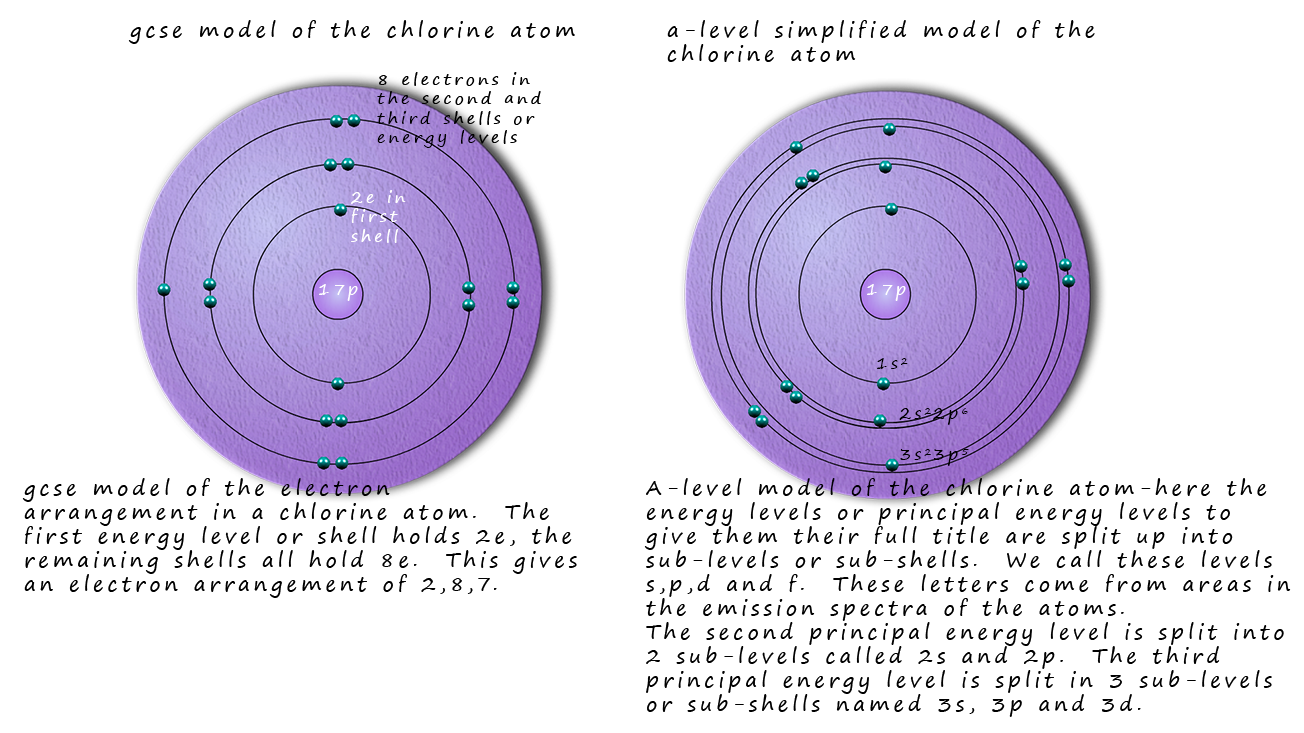
However when the emission spectra of the elements is studied closely it is found that the main principle energy levels
within atoms are in fact split into smaller sub-shells or sub-levels. Evidence from the ionisation energies of the various atoms
also help confirm the existence of these sub-shells. So a better model for the electronic structure of atoms might be
similar to the one below, this shows an atom of chlorine.
The azimuthal quantum number (l)
- From Schrodinger's equations, the shapes of the s,p,d and f orbitals are defined from the next quantum number
called the azimuthal quantum number (l) (sometimes it is referred to as the angular momentum quantum number) - it
can have values from 0 to n-1. This quantum number will help define
the shape of the orbital. As mentioned above the value of this quantum number is traditionally given
the letters s, p, d and f e.g.
| Value for the azimuthal quantum number (l) |
0 |
1 |
2 |
3 |
| Sub-shell or sub-level notation |
s |
p |
d |
f |
The letters s, p, d and f are usually referred to as sub-shells or sub-levels
within the main or principal energy level (n).
So far we have the principal quantum number defining the energy level of the orbital,
the azimuthal quantum number defining it shape. The next quantum number we need to consider is called the
magnetic quantum number (ml)
The magnetic quantum number (ml)
This quantum number will define how the orbital is
orientated in 3-d space. It's values are taken from the azimuthal quantum number (l),
it can have values from -l to l, e.g. The table below gives the values for the quantum
numbers in the first four energy levels and the number of electrons in each principal energy
level or shell. Note an orbital can hold a maximum of 2 electrons.
| Principal quantum number (n) |
Azimuthal quantum number (defines shape of sub-shell, s,p,d,f)(l) |
Magnetic quantum number (ml defines how the orbital is directed in 3d space |
Orbital |
Number of orbitals in each sub-shell |
Total number of electrons in shell or energy level |
| 1 |
0 |
0 |
1s |
1 |
2 |
| 2 |
0
1 |
0
-1, 0, 1 |
2s
2p |
1
3 |
8 |
| 3 |
0
1
2 |
0
-1, 0, 1
-2, -1, 0, 1, 2 |
3s
3p
3d |
1
3
5 |
18 |
| 4 |
0
1
2 |
0
-1, 0, 1
-2, -1, 0, 1, 2
-3, -2, -1, 0, 1, 2, 3 |
3s
3p
3d
4f |
1
3
5
7 |
32 |
You can see that each main energy level or shell (n) is split up into a number of sub-shells (l).
The number of orbitals in each sub-shell depends on the value of ml. If ml has a value of 1 then
this sub-levels contains 3 orbitals, called p-orbitals. If ml has a value of 2 then this sub-levels
contains 5 orbitals, called d-orbitals. Remember each orbital, no matter how big or small it is can only
hold a maximum of 2 electrons. The total number of orbitals in any one electron shell is simply found from
n2 and since each orbital holds 2 electrons the total number of electrons in any shell is simply
2n2.
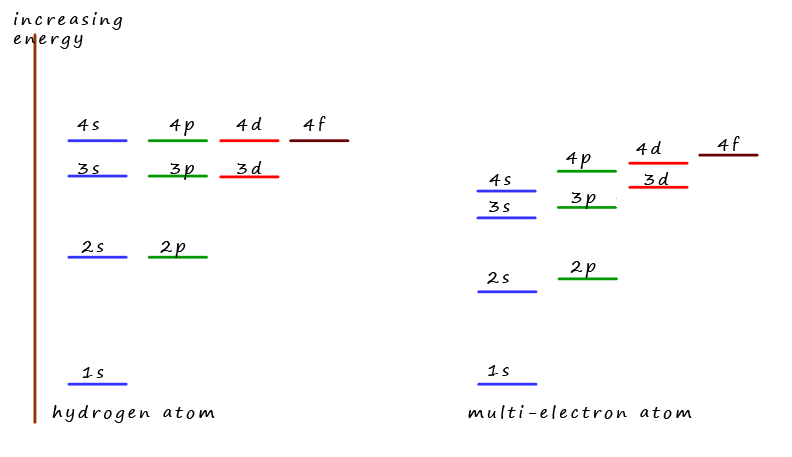
The diagram opposite shows the energies of the orbitals in one electron atoms such as hydrogen or He+.
Here all the orbitals in the same shell (same principal quantum number) are degenerate (have the same energy).
However in multi-electron atoms orbitals within the same energy level are no longer degenerate. Indeed there
is even some cross-over between orbitals in different shells e.g. the 4s sub-level is lower in energy than the
3d sub-level.
Next



