The ideal gas equation

From the page on the gas laws we have:
Boyles's law : V ∝ 1/p (constant n,T)
Charles's law : V∝ T (constant n, p)
Avogadro's law : V ∝n (constant p, T)
We can combine these 3 gas laws into one general equation:
V ∝ nT/p
We can also write this as:
V=R(nT/p) where R is a constant
We can rearrange this to give:
PV = nRT
This equation is called the ideal gas equation. The term R is called the
gas constant and
its units will depend upon the units of p (pressure),T (temperature)
and V (volume), n (number of moles), though the
temperature must always
be in degrees Kelvin. However when the volume, V is in cubic metres (m3),
temperature, T in Kelvins(K), pressure in pascals (Pa)
the value of R is 8.31 JK-1mol-1, these are the systeme Internationale (SI units) for p, T, n and V.
The kinetic theory of gases
The ideal gas equation describes the behaviour of an ideal gas.
An ideal gas is one where its behaviour will
follow the kinetic theory or model. This is a model developed by scientists to
help explain the properties and
behaviour of gases. It should be noted that
the kinetic theory is a model of how an ideal gas will behave.
It has a number of assumptions, these include:
- Gases consist of particles that move in
a totally random way.
- The volume of the particles in a
gas are negligible when compared the total volume
of the gas.
That is gases are mostly empty space.
- There are no intermolecular or attractive forces between the
particles in a gas.
- The gas particles collide with each
other and the walls of any container in totally
elastic collision (that is one in which no kinetic energy is lost).
- The average kinetic energy of the gas
particles is proportional to the temperature
of the gas.
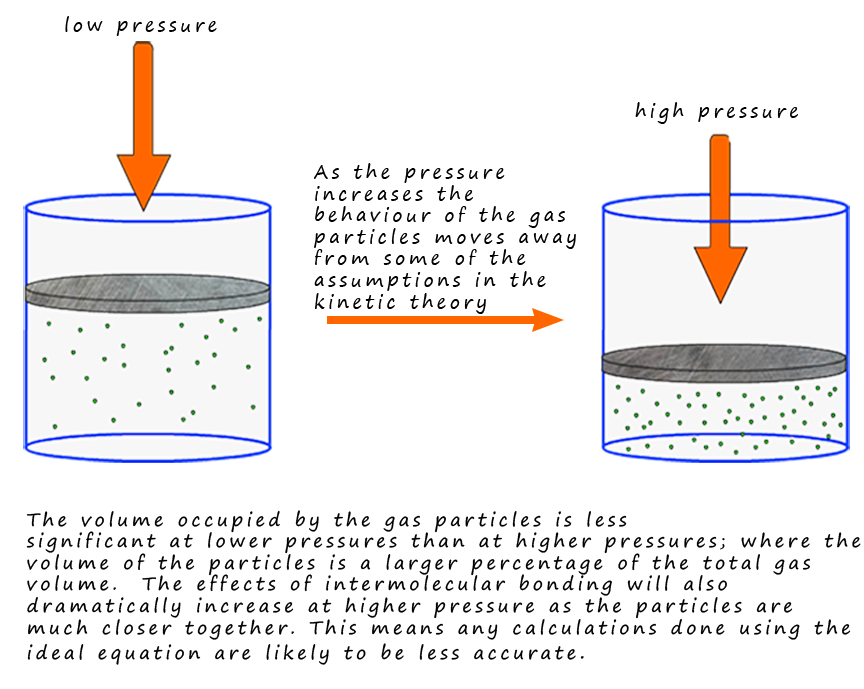
The behaviour of "real" gases can vary from that of an
ideal gas under certain conditions. For
example, one of the assumptions of the kinetic theory is that there
are no intermolecular
forces between the particle. When gases
are at a low pressure the particles will be
spread
out and the intermolecular forces between them are likely to be small.
However as the pressure
increases the particles will be forced
closer together and the effects of intermolecular bonding
are likely to become much stronger and more significant which will mean
that the behaviour of
the gas can no longer be described as ideal.
At higher pressures the densities of the gas
particles
will also increase massively and the assumption that the volume of the particles
is negligible compared
to the total volume of the gas
is also likely not to be true. This will mean that for example the
volume of a gas at high pressure
calculated from the ideal gas equation is likely to be much higher
than its actual volume.
Using the ideal gas equation
You should complete a few questions to ensure that you are confident and will be able to answer
any questions on the ideal
gas equation which appear in your exam. Check your understanding by doing clicking the link below to complete
the practice questions. The main problems students have with the
ideal gas equation is the units. The
exam board are likely to use the value of 8.31 JK-1mol-1 for R, the gas constant.
This means that you must use the
following units for the other variable:
- The volume(V) must be in cubic metres (m3). It is highly
likely that the volume in the exam is likely to be in
ml/cm3 or dm3. In this case you will need to convert these units into cubic metres. Remember
there is 1000 litres or
1000dm3 in a cubic metre. There are 1 million cubic centimetres (cm3) in a cubic metre.
- The temperature(T) must be in degrees Kelvin.
- The pressure(p must be in pascals. If you are given a pressure
in kPa (kilopascals) then you must convert this into pascals (Pa).
Calculating Mr using the ideal gas equation
You maybe asked in the exam to calculate the Mr
of an unknown gas or volatile liquid using the ideal gas equation.
This simply
requires a bit of simple arithmetic to rearrange the ideal gas equation.
We already know that:
Number of moles = mass/(mass of 1 mole)
or
n= m/Mr
So substituting for n in the ideal gas equation we have:
pV= mRT/Mr
One method which could be used is described below in the diagram.

So using a simple gas syringe and an accurate sensitive balance we can find m (the mass of the gas), temperature
will simply be room temperature, pressure will be atmospheric, R is 8.31, the gas constant. So all we have to do is
rearrange the ideal gas equation from above:
pV= mRT/Mr
Rearranging to make Mr the subject of the formula gives
Mr= mRT/pV
Practice questions
Next




